2D Logistic-adjusted-Sine map
Introduction
Because many significant properties of “chaos” can be found counterparts in cryptography, chaos theory is widely used in image security. This paper introduces a two-dimensional (2D) Logistic-adjusted-Sine map (2D-LASM). Performance analysis shows that 2D-LASM has better ergodicity and unpredictability, and a wider chaotic range than other existing chaotic maps. Using 2D-LASM, an image encryption scheme (LAS-IES) is also proposed. In LAS-IES, the principles of diffusion and confusion are strictly followed, and a structure of adding random values to the plaintext image is designed to ensure that each encrypted result is different and unpredictable. Simulation results and security analysis show that LAS-IES has excellent properties and can efficiently encrypt different kinds of images with a high security level for network media services.
2D Logistic-adjusted-Sine map
The 2D Logistic-adjusted-Sine map (2D-LASM) is defined by
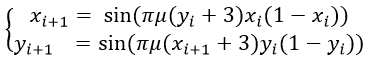 |
Where parameter μϵ[0,1].
Figure 1 shows the bifucation diagram of 2D-LASM.
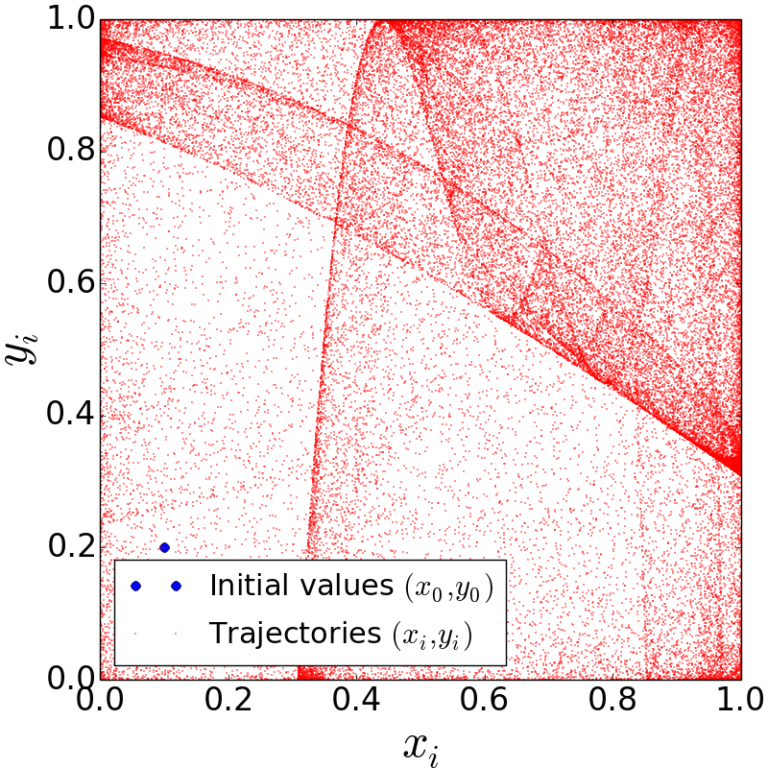 |
| Figure 1. The bifurcation diagram of 2D-LASM. |
2D-LASM-based image encryption scheme
Using 2D-LASM, this section proposes a new 2D-LASM-based image encryption scheme (LAS-IES), whose structure is shown in Figure 2. As can be seen, the security key is used to set the initial conditions of 2D-LASM to generate chaotic matrices $S_1$ and $S_2$. Random values are first added to the surroundings of the plaintext image. Bit manipulation confusion and bit manipulation diffusion are then designed to shuffle the pixel positions and change pixel values, {\color{blue}respectively}. After two rounds of bit manipulation confusion and diffusion, a plaintext image can be encrypted into an unrecognized random-like ciphertext image with a high security level.
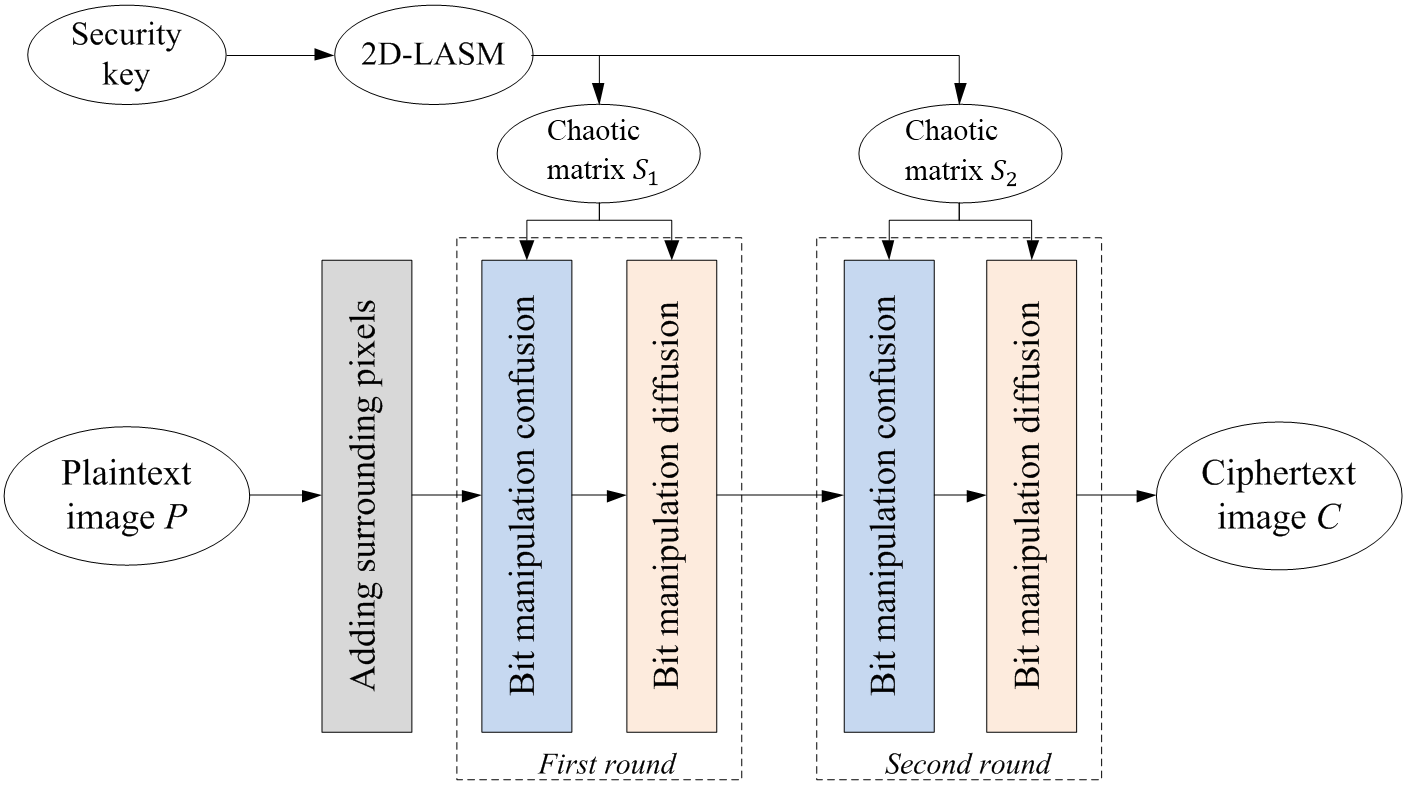 |
| Figure 2. The structure of image encryption algortihm. |
Advantages
Because 2D-LASM has extremely excellent chaos performance, random values are added to the surroundings of the plaintext image, and the confusion and diusion principles are strictly followed, the proposed LAS-IES has many advantages, which include but are not limited to:
- It has excellent performance to resist the chosen-plaintext, dierential, statistic and other widely used attacks. This is because, using the same security key to encrypt an image several times, the encrypted results are random-like and totally dierent from each other. This goes against many basic principles of cryptanalysis methods and thus makes them noneective.
- It can achieve good diusion and confusion performances since the diusion and confusion principles are strictly followed.
- It can achieve a fast encryption/decryption speed. This is because LAS-IES uses only two rounds of confusion and diffusion operations in the bit level.
- It has good reliability that can resist the noise or data loss attack. Even if the ciphertext images are with noise or loss some data, LAS-IES can still reconstruct the original image with high visual quality.